C++Guns – RoboBlog blogging the bot

Shortcut links:
Basic graph definitions (this page)
Basics of shortest paths

Gerichtete und ungerichtete Graphen

1. Ein gerichteter Graph 𝐺 = (𝑉, 𝐴) besteht aus einer endlichen Menge 𝑉 von Knoten und einem multiset 𝐴 von geordneten Paaren von Knoten. Die Elemente von 𝐴 sind die gerichteten Kanten von 𝐺.
2. Ein ungerichteter Graph 𝐺 = (𝑉, 𝐸) besteht aus einer endlichen Menge 𝑉 von Knoten und ein multiset 𝐸 von ungeordneten Paaren von Knoten. Die Elemente von 𝐸 sind die ungerichteten Kanten von 𝐺.
3. Ein gerichteter oder ungerichteter Graph ist simple (einfach), wenn:
   • Kein Knoten, in 𝐴 oder 𝐸, mit sich selbst verbunden ist
   • Die multisets 𝐴 oder 𝐸 sind nur sets
4. Ein gerichteter Graph 𝐺 = (𝑉, 𝐴) ist
   • symmetrisch, wenn (𝑣,𝑤) ∈ 𝐴 impliziert (𝑤,𝑣) ∈ 𝐴
   • anti-symmetrisch, wenn (𝑣,𝑤) ∈ 𝐴 impliziert (𝑤,𝑣) ∉ 𝐴

Adjacency, incidence, degree (benachbart, verbunden, Grad)

1. Zwei Knoten eines gerichteten oder ungerichteten Graphen heißen adjacent (benachbart), wenn sie mindestens eine gemeinsame Kante haben.
2. Ein Knoten und eine Kante heißen incident (verbunden), wenn der Knoten zu der Kante gehört.
3. Zwei Kanten heißen incident (verbunden), wenn sie mindestens einen gemeinsamen Knoten haben.
4. Für einen Knoten, die Anzahl der incident (verbundenen) Kanten ist der Grad von diesem Knoten. Ein Knoten mit Grad 0 heißt isoloert.
5. Betrachte einen gerichteten Graph 𝐺 = (𝑉, 𝐴):
   1. Für eine Kante 𝑎 = (𝑣,𝑤) ∈ 𝐴, 𝑣 ist der tail (Fuß,Startknoten) von 𝑎 und 𝑤 ist der head (Kopf/Endknoten) von 𝑎.
   2. Eine Kante 𝑎 = (𝑣,𝑤) ∈ 𝐴 ist eine outgoing (abgehende) Kante von 𝑣 und eine incoming (eingehende) Kante von 𝑤.
   3. outdegree von einem Knoten 𝑣 ∈ 𝑉 ist die Anzahl der abgehenden Kanten.
   4. indegree von einem Knoten 𝑣 ∈ 𝑉 ist die Anzahl der eingehenden Kanten.

Transpose of a graph

Für einen gerichteten Graph 𝐺 = (𝑉, 𝐴), die transpose (Vertauschung) von 𝐺 ist das Ergebnis vom Drehen aller Kanten von 𝐺. (Start- und Zielknoten tauschen)

Subgraph

1. Gegeben sind zwei einfache, ungerichtete Graphen 𝐺₁ = (𝑉1, 𝐸1) und 𝐺2 = (𝑉2, 𝐸2).
   Dann ist 𝐺1 ein subgraph von 𝐺2, wenn es eine Knotenteilmenge 𝑉' ⊆ 𝑉2 gibt und eine bijektive (umkehrbare) Funktion φ: 𝑉1 -> 𝑉' gibt, welche alle Knoten aus 𝑉1 auf die Teilmenge 𝑉' von 𝑉2 abbildet, und zwar genau so, dass eine Kante {𝑣,𝑤} aus 𝐸1 impliziert, dass es eine andere Kante {φ(𝑣),φ(𝑤)} ∈ 𝐸2 gibt.
   Denn es müssen nicht nur alle Knoten von 𝑉1 in 𝑉2 zu finden sein, sondern natürlich auch alle Kanten.
2. Gegeben sind zwei einfache, gerichtete Graphen 𝐺₁ = (𝑉1, 𝐴1) und 𝐺2 = (𝑉2, 𝐴2).
   Dann ist 𝐺1 ein subgraph von 𝐺2, wenn es eine Knotenteilmenge 𝑉' ⊆ 𝑉2 gibt und eine bijektive (umkehrbare) Funktion φ: 𝑉1 -> 𝑉' gibt, welche alle Knoten aus 𝑉1 auf die Teilmenge 𝑉' von 𝑉2 abbildet, und zwar genau so, dass eine Kante (𝑣,𝑤) aus 𝐴1 impliziert, dass es eine andere Kante (φ(𝑣),φ(𝑤)) ∈ 𝐴2 gibt.
   Quasi das selbst wie für ungerichtete Grapen.
3. Ein spanning subgraph von einem ungerichteten oder gerichteten Graphen 𝐺 ist ein subgraph welcher alle Knoten von 𝐺 enthält.
   Aber nicht alle Kanten (es bildet sich ein Baum).

Paths

1. Ein ordinary (gewönlicher) Path in einem ungerichteten Graphen ist eine endliche, geordnete Sequenz ({v₁,v₂}, {v₂,v₃}, ..., {v_k-2, v_k-1}, {v_k-1,v_k}) von Kanten.
2. Ein ordinary (gewöhnlicher) Path in einem gerichteten Graphen ist eine endliche, geordnete Sequenz ((v₁,v₂), (v₂,v₃), ..., (v_k-2, v_k-1), (v_k-1,v_k)) von Kanten.
3. Ein generalized a.k.a. weak (genereller, schwacher) Path in einem gerichteten Graphen ist eine endliche Sequenz ((v₁,w₁), (v₂,w₂), ..., (v_k-1, w_k-1), (v_k,w_k)), so dass drehen von einigen Kanten einen ordinary Path ergibt (Ein ordinary Path ist schon ein generalized Path bei dem keine Kanten gedreht werden müssen).
4. Ein Path ist simple (einfach) wenn er keine Knoten doppelt enthält.
5. Ein Knoten 𝑡 ∈ 𝑉 ist reachable (erreichbar) von 𝑠 ∈ 𝑉, wenn es einen Path von 𝑠 nach 𝑡 in dem Graph gibt.
   Abhängig vom Kontext, der Path muss ein ungerichteter, ein gewöhnlicher gerichteter, oder ein generalized Path sein.
   Jeder Knoten ist von sich selbst aus erreichbar, via den trivialen Path welcher nur diesen Knoten enthält und sonst keine Kanten.
6. Die internal (internen) Knoten von einem Path jeglicher Art sind alle Knoten von diesem Path außer dem Start und Endknoten.
   (Wenn der Start oder Endknoten mehr als einmal im Path vorkommt, zählt es zu den internen Knoten)
7. Zwei Pathe sind edge-disjoint (disjunkt) wenn sie keine gemeinsame Kante haben. Sie sind (internally) node-disjoint wenn sie keine gemeinsamen Knoten haben.

Cycles

1. Ein (ordinaty/gewöhnlicher) cycle in einem ungerichteten Graphen ist eine endliche, geordnete Sequenz ({v₁,v₂}, {v₂,v₃}, ..., {v_k-2, v_k-1}, {v_k-1, v₁} ) von Kanten. In anderen Worten: Ein cycle ist ein Path, so dass der Startknoten gleich dem Endknoten ist.
2. Ein (ordinaty/gewöhnlicher) cycle in einem gerichteten Graphen ist eine endliche, geordnete Sequenz ((v₁,v₂), (v₂,v₃), ..., (v_k-2, v_k-1), (v_k-1, v₁) ) von Kanten. In anderen Worten: Ein cycle ist ein Path, so dass der Startknoten gleich dem Endknoten ist.
3. Ein generalized a.k.a. weak (genereller, schwacher) cycle in einem gerichteten Graphen ist eine endliche Sequenz ((v₁,w₁), (v₂,w₂), ..., (v_k-1, w_k-1), (v_k,w_k)), so dass drehen von einigen Kanten einen ordinary cycle ergibt (Ein ordinary cycle ist schon ein generalized cycle bei dem keine Kanten gedreht werden müssen).
4. A cycle is simple if no proper part is a cycle of its own.
5. Ein gerichteter oder ungerichteter Graph ist acyclic (cycle-free), wenn er kein ordinary cycle enthält. Ein gerichteten Graphen nennt man in diesem Fall DAG (directed acyclic graph).
6. Für zwei Knoten 𝑠,𝑡 ∈ 𝑉, ein (s,t)-graph 𝐺 = (𝑉, 𝐴) ist ein DAG, so dass 𝑠 ist der einzige Knoten mit indegree 0, und 𝑡 ist der einzige Knoten mit outdegree 0.
   Ein DAG ist ein (s,t)-Graph , genau dann, wenn der Graph G die Vereinigung von (nicht notwenigerweise internally Knoten oder Kanten disjunkt) allen (s,t)-pathen ist.

Forests, trees, branchings, arborescences

1. Ein forst ist ein cycle-free undirected Graph. Disconnected nicht vergessen sonst macht es kein Sinn.
   
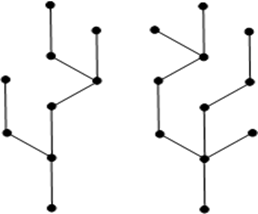
2. Ein tree ist ein conected forst. Also connected, cycle-free undirected Graph.
   
   Das ist nicht unbedingt das, was man von der Schule her noch kennt. In der Schule war ein tree immer ein directer Graph mit einem Wurzelknoten. Aber gut. Muss ja nicht.
3. Ein branching ist ein cycle-free, directed Graph, so dass indregree für jeden Knoten 0 oder 1 ist. Das sieht gedanklich schon ehr wie ein Baum aus. Aber noch nicht ganz. Directed muss sein, klar. Sonst könnte man seine "Entscheidungen" beim "branchen" ja zurück nehmen.
4. Eine arborescene ist ein branching, so dass genau ein Knoten indegree 0 hat. Das nennt man auch rooted trees und der einzigartige Knoten mit indegree 0 ist root. DAS ist ein Baum.
5. Ein forest/tree/branching/arborescence in einem Graphen G ist ein Subgraph von G welcher wiederrum ein forest/tree/branching/arborescence ist.
   Naja, auf dem zweiten Blick stimmt das. Jeden Subgraph den man aus einem Tree rausholt ist wieder ein Tree.

Connectedness

Types of connectedness:

Types of connectedness:
1. Ein ungerichteter Graph ist connected, wenn jedes mögliche Knotenpaar durch einen Path verbunden ist.
2. Ein ungerichteter Graph ist k-connected, wenn jedes mögliche Knotenpaar mindestens durch k internally node-disjoint Pathe verbunden ist. Einfach nur connected ist 1-connected. k=2 ist biconnected.
3. Ein directed Graph ist weakly connected, wenn für jeden Knotenpaar ein generalized path existiert welcher diese Knoten verbindet.
4. Ein directed Graph ist strongly connected, wenn für jedes geordnerte Knotenpaar ein ordinary path den ersten mit den zweiten Knoten verbindet.

Links:

5. Ein articulation Knoten in einem connected undirected Graph ist so ein Knoten, dass wenn der Knoten (und die angeschlossenen Kanten) entfernt wird, der Graph disconnected wird.
6. Eine bridge in einem connected undirected Graph ist eine Kante, so dass der Graph disconnected wird wenn diese Kante entfernt wird.

Connected components:

7. Die k-connected componenten von einem ungerichteten Graphen 𝐺 = (𝑉, 𝐸) ist die inclusion-maximal Knotenmengen 𝑉' ⊆ 𝑉, so dass der Subgraph von 𝐺, hergestellt von 𝑉', k-connected ist (d.h. wenn jedes mögliche Knotenpaar in V' mindestens durch k internally node-disjoint paths miteinander verbunden sind).
   For k=1 wir sagen connected und für k=2 wir sachen biconnected compoenten von G.
8. Die weakly und strongly connecten componenten von einem directed Graph 𝐺 = (𝑉, 𝐴) sind die inclusion-maximal Knotenmengen 𝑉' ⊆ 𝑉, so dass der Subgraph von 𝐺 induced von 𝑉' ist weak und strong connected.

Bipartite and k-partite graphs

Sei 𝐺 = (𝑉, 𝐸) ein ungerichteter Graph.

1. Der Graph 𝐺 ist 𝑘-partite, wenn es eine 𝑘-partition {𝑉₁, ..., 𝑉_k} von 𝑉 gibt, so dass {𝑣,𝑤} ∉ 𝐸 ist für jedes Paar 𝑣,𝑤 ∈ 𝑉_i für jedes i ∈ {1,...,𝑘}.
2. Für 𝑘=2 wir sagen 𝐺 ist bipartite.

Statement: Ein verbundener, ungerichteter Graph ist bipartite, genau dann wenn es kein Cycle von ungerade Länge gibt.
Das lässt sich leicht erkennen, wenn man die Knoten auf dem Path abwechseln V1 und dann V2 zuordnet. Bei ungeraden Längen sind die Knoten der letzten Kante bei immer aus V1 oder V2.

Complete graphs

1. Für eine positive ganzzahlige Nummer 𝑛, der complet graph 𝐾_𝑛 = (𝑉,𝐸) ist der einzigartige undirecte Graph, so dass |𝑉| = 𝑛 und alle (ungeordneten) Paaren of Knoten in 𝐸 sind. Das heisst jeder mit jedem. Dense.
2. Für positive ganzzahlige Nummern 𝑚 und 𝑛, der complete bipartite graph 𝐾_𝑚,𝑛 = (𝑉₁ UNITED 𝑉₂, 𝐸) ist der einzigartige undirecte graph, so dass |𝑉₁| = 𝑚 und |𝑉₂| = 𝑛 und jeder (ungeordnete) Pair {𝑣,𝑤} mit 𝑣 ∈ 𝑉₁ und 𝑤 ∈ 𝑉₂ in 𝐸 ist.
   Also jeder von dem einem mit jeder von dem anderen.